凯发k8游戏官网入口在非对称溉场中的用问题。通过GAMBIT前处理软件建立管道及流量计的物理模型,并利用FLUENT进行管道内水动的仿真计算。选取等值面观察管道内溉体的速度、压力等物理量的云图,失量图等可视化图像。通过图像分析得出结论,直管道部分的场分布均匀,而管道转弯处的场由于压力的作用,产生了非对称场。靠近弯管道内径的水产生了高速场,明显高于外径的水速度。因此要在弯管部分进行多点测量,以修正流量计在非对称流场中的测量准度。随着近些年来我国流量测量水平的发展,越来越多种类的流量计广泛应用于各种行业。其中,作为电磁流量计中一个种类的插入式电磁流量计,由于其自身结构的轻巧,安装拆卸便捷,相比制造费用较高,安拆与维修都很不便的普通电磁流量计而言具有非常大的优势,从而广泛应用于现在的机械工业大口径管道的流量检测中。在国际上,由于目前能源与环保计量方面的需求越来越大,如机械、化学工业污水流量的测量等,各国家发展插入式流量计已经成为一种趋势。我国的插入式电磁流量计的研究还在上升;对于测量精度的提高和实物的改进还有着很大的提升空间,尤其是在管道排布复杂、弯管多、角度大的工业现场,即在非对称流场下的应用还需做深入探讨。理相同,插入式电磁流量计的测量原理同样是基宇法拉第电磁感虛定律。通过对目标流场内某一点流速的测,经过一系列计算推导后,得出整个目标流场的平均流速。所以说插入式电磁流量计是一种点流速的了流量计。以管道流速测量为例,测量流场时凯发k8,将流量计以平行Z轴,垂直于XOY面方向插人管遒内部,感应电极位位于流量计尾端两侧,与水流方向保持垂直,且同属XOY面。水流流经流量计时,做切割磁感线运动,由法拉第电磁感应定律可知,磁场中会产生电动势E=BD`n表示管道横截面平均流速。
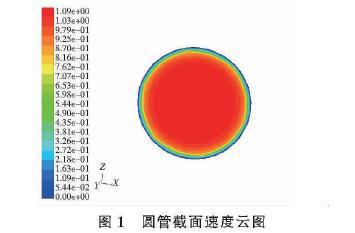
可知感应电.动势E和流量Q是线性关系,与流场内其他变化的物埋无关。即可以通过流量计对电信号的捕捉来实现对流场流量的检测。2 数值计算方法FLUEST软件主要包括前处理器GAMBIT和后赴理器FLUEST两部分,二者相辅相成,缺一不可。2.1前处理GAMBIT建模仿真计算前,首先进行仿真的前处理,即运用 GAMBIT几何建模,之后对所建模进行网格的划分和生成,谁知完边界条件后输出mesh文件。把mesh文件导入到FLUENT中进行流体仿线后处理FLUENT仿真计算求解计算有以下几个步骤:检查导入模型的网格,选择计算模定义流体材料性质,设置边界条件,求解方法及其控制,迭代计算,检查保存并分析仿线数值模掀仿线对称流场直管道中的仿线圆管流动仿真首先在GAMBIT中简历半径0.1m,长度4m的长直圆管物理模型采用六面体网格划分管道模型,如图1所示。定义边界条件后输出mesh文件,启动FLUENT仿真计算。迭代计算后,查看结果,通过图1可以看出圆管内的速度值程同心圆分布,越靠近中心处速度越大,在靠近管壁的区域,速度几乎为零。管道内的流速稳定正常。
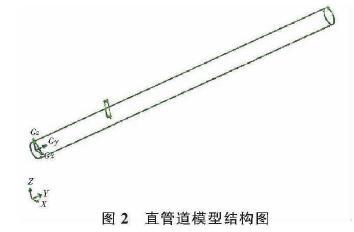
运用GAMBIT建模划分网格,其中在体网格的划分上Element选择Hex,Type选择Cooper凯发k8。管道模型最终划分成的网格如图3所示。定义水流的入口及出口,流量计模型位于左侧水流入口处1m位置。导入FLUENT求解计算。定义求解器定水的流速设置为1m/s。迭代计算后,输出结果图组。

由于三维模型的计算结果不方便查看,所以通过创建电极所在的等值面来观察电极所在区域周围的流场,选取Z=0.06m平面来输出压力和速度等值线及云图。选择速度云图放大观察,如图4所示。
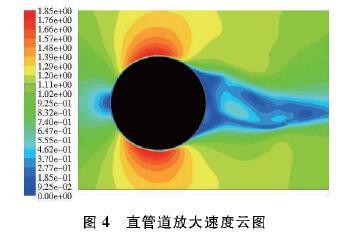
根据选取面放大后的速度云图观察可以看出,水流流经流量计的时候,两侧的电极周围的流场受圆柱绕流影响,产生了高速流场,水流无法很好地贴合流量计后半段壁面流动,致使流速减小,边界层出现分离,产生尾涡流区。尾涡区在一定程度上破坏了周围流场的稳定性。由于传统型插入式电磁流量计的自身形状不可避免的会对所测流场产生一定干扰,因此需要采用机械工艺方面的设计对其自身物理结构进行改良。
保持直管部分与之前的尺寸不变,弯管处采用半径4倍管径即0.4m的90°弯管。简历物理模型,如图5所示,划分网格,设定边界条件后求解。
迭代计算后,观察输出的速度云图和压力云图,如图6和图7所示。可以看出弯管处出现了压力降,内径速度明显大于外径。再通过放大的速度矢量图可以看出,转弯处的内径高速水流沿外径流出,并且速度下降逐渐恢复转弯钱的速度,出弯后的内径部分几乎无流速,经过一定管长后恢复匀速。

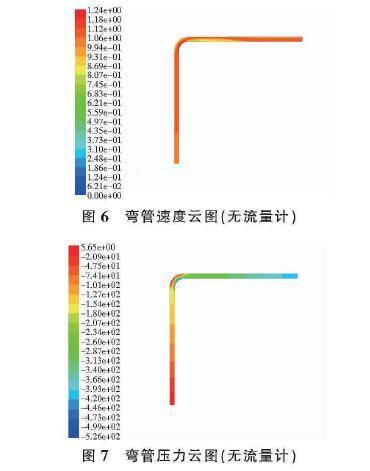
在多数现场环境下,长直管较少,短直管居多,然而接近弯管处的流体分布是不对称拟合流场,这与对称流场下的多点流速泄露及数据分析会有较大出入,因此在弯管部分的检测要重新选取不同的点进行检测。保留上一小节中弯管道物理模型不变,以水流流向作参考,在靠近弯管入口和出口0.1m处分别插入流量计模型,进行多次测量,除了流量计插入位置其余物理量保持不变。
由于现场实际情况中,工业管道会按照现场需要进行安置排布,即横向竖向多角度转弯,管内流体是湍流流动,流场基本上是不定常的,因此在定义求解器时,要用非稳态的求解器进行模拟计算,即在Time选项中选择非定常Unsteady。其他计算模型设定,管内湍流模型分布方程的离散模式设定为k-epsilon即二阶迎风差分格式,并采用SIMPLEC算法进行修正。然后定义管道内的流体材料,本次仿真实验使用液态水为管道内的流体。在材料下拉列表中选择,water-liquid(h201)边界条件,inlet入口边界条件定义水流速为1m/s。湍流强度Turbulent Intensity和水力直径Hydraulic Diameter选项分别输入5和0.04。设置求解参数,初始化及残差图后,保存文件进行迭代计算。迭代计算后,残差图均呈收敛状态。选择Z=0.06m平面分别观察速度及压力云图。流量计在靠近弯管入口处0.1m的输出结果如图8和9所示。
可以看出转弯处依旧出现压力降,由于压力的作用,在水流在内径的速度大于外径,流量计两侧产生告诉流场,两侧电极可以检测到明显的信号,但由于内外径流速的不同,两电极所检测的信号有一定量差,流量计尾部速度几乎为零。

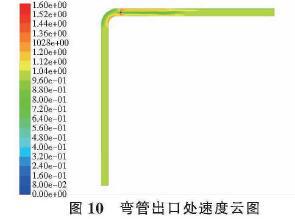
流量计的尾涡区对水流出弯后的直管部分流场有一定的影响,流量计电极两侧所检测到的信号由于弯管处压力降的作用存在量差,并且速度要略大于入口处。
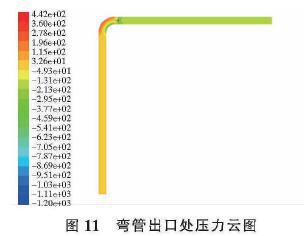
经过以上对比实验证明,需要在弯道入口及出口部分选取垂直与XOY面不同深度的点来进行测量,从而得到流量计在非对称条件下测速的理想修正函数。(1)通过多次实验,分析仿真结果,对物理模型网格的划分精度及参数的调整校正,最终使残差图呈现收敛状态。通过对输出图组的观察分析,基本准备模拟出管道中的流场分布,同事得出插入式电磁流量计对流场分布影响。
(3)由于圆柱型的流量计的尾流对所测流场稳定性有一定影响,可以通过机械工艺加工对流量计的外形进行改良,尽可能减少尾流,保证流场的稳定性。